OF5版本以后重心坐标与绝对坐标的相互转换的问题。

上级

最近在研读OpenFOAM中particle类的barycentric coordinates 和global coordinates转换矩阵的程序，遇到一点问题，现总结出来和大家讨论一下。
OF5.0以后对颗粒追踪采用了barycentric方法，目的是更好的捕捉颗粒轨迹与tetrahedra网格面的交点，四面体内任意一点$\mathbf{p}$的global coordinates 可以表示为barycentric coordinates ($\lambda_i$)与顶点的乘积和：
\begin{equation}
\label{eq:barycentric coordinates}
\mathbf{p}=\sum_{i=1}^{4}\lambda_i\mathbf{v_i}
\end{equation}
其中$\mathbf{v_i}$是四面体顶点坐标。
示意图如下：

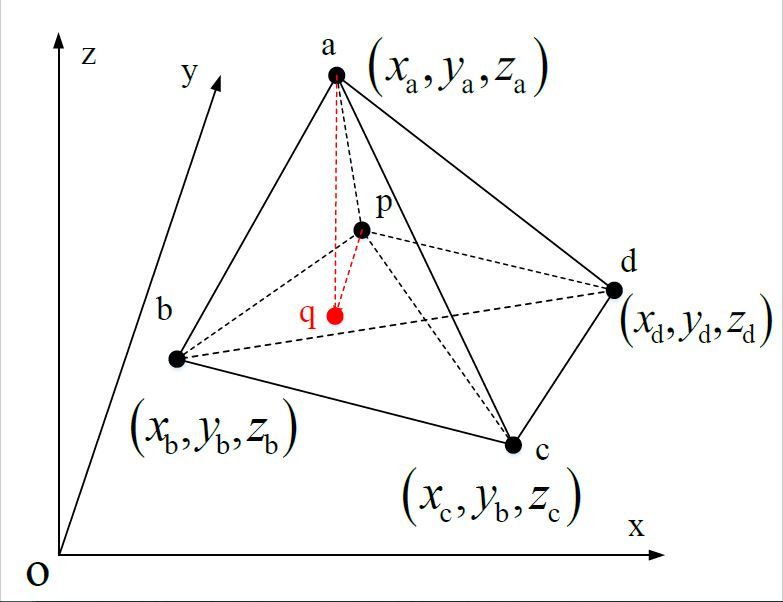
如上图，四面体中有一点$\mathbf{p}$，则$\mathbf{p}$点的重心坐标（$\lambda_1,\lambda_2,\lambda_3,\lambda_4$）的计算方法为点$\mathbf{p}$将四面体分成的四个小四面体与大四面体的体积之比:
\begin{equation}
\label{eq:lambda1}
\lambda_{1}=\frac{V_{\rm{pbcd}}}{V_{\rm{abcd}}}=1-\lambda_{2}-\lambda_{3}-\lambda_{4},
\end{equation}
\begin{equation}
\label{eq:lambda2}
\lambda_{2}=\frac{V_{\rm{pacd}}}{V_{\rm{abcd}}}=\frac{6V_{\rm{pacd}}}{6V_{\rm{abcd}}}=\frac{\mathbf{ap}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)};,
\end{equation}
\begin{equation}
\label{eq:lambda3}
\lambda_{3}=\frac{V_{\rm{pabd}}}{V_{\rm{abcd}}}=\frac{6V_{\rm{pabd}}}{6V_{\rm{abcd}}}=\frac{\mathbf{ap}\cdot\left(\mathbf{ad}\times\mathbf{ab}\right)}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)}，
\end{equation}
\begin{equation}
\label{eq:lambda4}
\lambda_{4}=\frac{V_{\rm{pabc}}}{V_{\rm{abcd}}}=\frac{6V_{\rm{pabc}}}{6V_{\rm{abcd}}}=\frac{\mathbf{ap}\cdot\left(\mathbf{ab}\times\mathbf{ac}\right)}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)}，
\end{equation}
其中 $V_{\rm{pbcd}}$, $V_{\rm{pacd}}$, $V_{\rm{pabd}}$, 和 $V_{\rm{pabc}}$ 是小四面体的体积, $\mathbf{ap}=\mathbf{p}-\mathbf{a}$, $\mathbf{ab}=\mathbf{b}-\mathbf{a}$, $\mathbf{ac}=\mathbf{c}-\mathbf{a}$, $\mathbf{ad}=\mathbf{d}-\mathbf{a}$.
定义从barycentric coordinates到global coordinates的转换矩阵$\mathbf{A}$，则
\begin{equation}
\begin{aligned}
\label{eq:barycentric to global}
\mathbf{p}=\mathbf{A}\boldsymbol{\lambda}\left(\mathbf{p}\right)\rightarrow
\begin{bmatrix}x_{\rm{p}}\\y_{\rm{p}}\\z_{\rm{p}}\end{bmatrix}=
\begin{bmatrix}x_{\rm{a}}&x_{\rm{b}}&x_{\rm{c}}&x_{\rm{d}}\\y_{\rm{a}}&y_{\rm{b}}&y_{\rm{c}}&y_{\rm{d}}\\z_{\rm{a}}&z_{\rm{b}}&z_{\rm{c}}&z_{\rm{d}}
\end{bmatrix}
\begin{bmatrix}\lambda_1\\
\lambda_2\\
\lambda_3\\
\lambda_4\end{bmatrix};.
\end{aligned}
\end{equation}
其中$\lambda_i$就是$\mathbf{p}$的重心坐标，矩阵$\mathbf{A}$就是由四面体各个顶点的global coordinates组成的坐标矩阵。
既然有了正向变换，同样需要逆向变换，定义一个逆向变换矩阵$\mathbf{T}=\left[\mathbf{bd}\times\mathbf{bc}\quad\mathbf{ac}\times\mathbf{ad}\quad\mathbf{ad}\times\mathbf{ab}\quad\mathbf{ab}\times\mathbf{ac}\right]$将global coordinates转换为barycentric coordinates:
\begin{equation}
\label{eq:global to barycentric}
\boldsymbol{\lambda}=\frac{\mathbf{ap}\cdot\mathbf{T}}{\rm{det}\mathbf{A}}=\frac{\left[\mathbf{ap}\cdot\left(\mathbf{bd}\times\mathbf{bc}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ad}\times\mathbf{ab}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ab}\times\mathbf{ac}\right)\right]}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)},
\end{equation}
公式\eqref{eq:global to barycentric}的四个组成成分其实就是上面的公式\eqref{eq:lambda1}，\eqref{eq:lambda2}，\eqref{eq:lambda3}，\eqref{eq:lambda4}。$\rm{det}\mathbf{A}$是矩阵$\mathbf{A}$的行列式，表示为$\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)$。
至此，barycentric coordinates与global coordinates的正向变换和逆向变化都已经定义完成了，上面的分析是基于我看OF6的代码以及查阅相关的文献总结出来的。
但是有一个问题困扰了我很久了，那就是逆向变换矩阵的第一个元素是：
\begin{equation}
\label{eq:the first element of T}
\boldsymbol{\lambda}_1=\frac{\mathbf{ap}\cdot\left(\mathbf{bd}\times\mathbf{bc}\right)}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)},
\end{equation}
这个和公式\eqref{eq:lambda1}的定义不同，因为分子上算的不是图中小四面体pbcd的体积，就这儿我无法理解为什么OF里要这么定义，并且我看OF5-OF8里面都是这么定义的，我觉得有点问题，所有发出来和大家讨论一下，我觉得我自己是解决不了这个问题了

李东岳

简直是大作！！我一直在想研究下这方面工作没倒出空来。我先留言学习一下，在讨论

感谢分享！！！！！！！

李东岳

首先跟随你的思想：按照理论，应该是：
\begin{equation}
\boldsymbol{\lambda}=\frac{\mathbf{ap}\cdot\mathbf{T}}{\rm{det}\mathbf{A}}=\frac{\left[\mathbf{bp}\cdot\left(\mathbf{bd}\times\mathbf{bc}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ad}\times\mathbf{ab}\right)\quad\mathbf{ap}\cdot\left(\mathbf{ab}\times\mathbf{ac}\right)\right]}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)},
\end{equation}
同时
\begin{equation}
\mathbf{bp}\neq\mathbf{ap}
\end{equation}
所以代码跟理论对不上？

上级

@东岳是的李老师，我的疑惑就在这儿，$\mathbf{bp}\neq\mathbf{ap}$，和代码对不上，细读代码发现不一样。

李东岳

问题解决了么？

上级

仔细读了代码，现在还剩最后一点小问题，其实说到底还是原来的问题，barycentric追踪是通过bary displacement元素的正负来判断颗粒运动轨迹与四面体网格面的交点的，例如这个图形
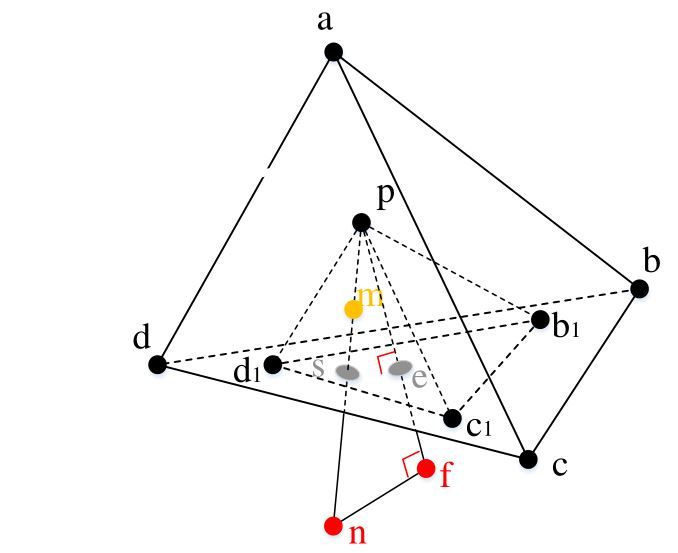
捕获.JPG
颗粒$\mathbf{p}$运动到$\mathbf{n}$，轨迹$\mathbf{pn}$与面$\underline{\rm{bcd}}$相交于点$\mathbf{s}$，那么矢量$\mathbf{pn}$的barycentric displacement的计算方法为：
\begin{equation}
\begin{aligned}
\label{eq:barycentric displacement}
\boldsymbol{\lambda}_{\mathbf{p}\rightarrow\mathbf{n}}
&=\boldsymbol{\lambda}\left(\mathbf{n}\right)-\boldsymbol{\lambda}\left(\mathbf{p}\right)=\frac{\mathbf{an}\cdot\mathbf{T}}{\rm{det}\mathbf{A}}-\frac{\mathbf{ap}\cdot\mathbf{T}}{\rm{det}\mathbf{A}}=\frac{\mathbf{pn}\cdot\mathbf{T}}{\rm{det}\mathbf{A}}\
&=\frac{\left[\mathbf{pn}\cdot\left(\mathbf{bd}\times\mathbf{bc}\right)\quad\mathbf{pn}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)\quad\mathbf{pn}\cdot\left(\mathbf{ad}\times\mathbf{ab}\right)\quad\mathbf{pn}\cdot\left(\mathbf{ab}\times\mathbf{ac}\right)\right]}{\mathbf{ab}\cdot\left(\mathbf{ac}\times\mathbf{ad}\right)};.
\end{aligned}
\end{equation}
此时barycentric dispalcement的符号为(-,+++)，可以判断轨迹与面$\underline{\rm{bcd}}$相交，同根根据$\mathbf{p}$和$\mathbf{n}$的barycentric coordinates可以求出点$\mathbf{s}$的barycentric coordinates，再转换为点$\mathbf{s}的$gobal coordinates，然后进如下一个四面体网格追踪。
上面我只是简述了颗粒在一个四面体网格内的追踪过程，从计算barycentric dispalcement的角度来看，逆向变换矩阵$\mathbf{T}$是没有问题的，但是问题还是在于从barycentric coordinates to global coordinates的过程，矩阵$\mathbf{T}$的第一个元素有问题。如果把\ref{eq: the first element of T}变为$\boldsymbol\lambda_1=1-\boldsymbol\lambda_2-\boldsymbol\lambda_3-\boldsymbol\lambda_4$就好了，但是程序里没有这么写，说到底还是原来的问题如果李老师有时间的话可不可以读一下particle类，我觉得您可以帮我释疑

上级

上面那个公式引用是公式（8）

BlookCFD

（7）这个公式确实是错的，但是particle里面都用的是(11)这个公式，用来计算“位移”的barycentric坐标，而不是点的barycentric坐标，OpenFOAM/meshes/primitiveShapes/tetrahedron/tetrahedronI.H有计算点的barycentric坐标，你可以比较下。

上级

@BlookCFD 谢谢您的指点，我有看了一眼程序，我理解错了，OF里面是通过计算barycentric displacement来获得barycentric coordinates的，我一直被src/lagrangian/basic/particle/particle.C里面的一句代码给误导了，现贴出来：

particle.C 1062-1096 OpenFOAM6
void Foam::particle::correctAfterInteractionListReferral(const label celli)
 {
     // Get the position from the barycentric data
     const vector pos(coordinates_.b(), coordinates_.c(), coordinates_.d());
 
     // Create some arbitrary topology for the supplied cell
     celli_ = celli;
     tetFacei_ = mesh_.cells()[celli_][0];
     tetPti_ = 1;
     facei_ = -1;
 
     // Get the reverse transform and directly set the coordinates from the
     // position. This isn't likely to be correct; the particle is probably not
     // in this tet. It will, however, generate the correct vector when the
     // position method is called. A referred particle should never be tracked,
     // so this approximate topology is good enough. By using the nearby cell we
     // minimize the error associated with the incorrect topology.
     coordinates_ = barycentric(1, 0, 0, 0);
     if (mesh_.moving())
     {
         Pair<vector> centre;
         FixedList<scalar, 4> detA;
         FixedList<barycentricTensor, 3> T;
         movingTetReverseTransform(0, centre, detA, T);
         coordinates_ += (pos - centre[0]) & T[0]/detA[0];
     }
     else
     {
         vector centre;
         scalar detA;
         barycentricTensor T;
         stationaryTetReverseTransform(centre, detA, T);
         coordinates_ += (pos - centre) & T/detA;
     }
 }

其中的这句代码

coordinates_ += (pos - centre) & T/detA;

其实前面已经先定义了

coordinates_ = barycentric(1, 0, 0, 0);

后面计算单点的barycentric coordinates其实还是用的barycentric displacement的概念来转换的。

困扰了我两周的问题终于解决了，现在异常开心，在此对@东岳和@BlookCFD 表示万分感谢。

CFD中文网

OF5版本以后重心坐标与绝对坐标的相互转换的问题。