关于MRF方法的理解的疑问
-
能不能将MRF理解为有一个新的速度场,该速度场是由绝对速度的速度场减去参考系的牵连速度得到的。该新的速度场运输了单位质量的流体,运输的物理量包括绝对速度的动量、温度、湍动能等。所以如果应用了MRF方法,界面的通量应该为相对速度的通量无论对于那个方程来说(动量,能量,质量,湍流物理量,sclar transport equation )。 请问我理解的对吗
-
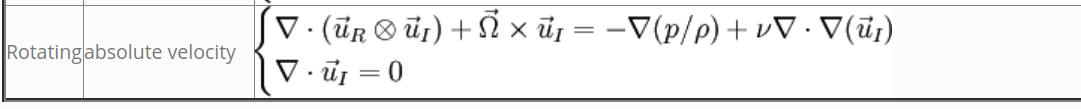
cited:http://openfoamwiki.net/index.php/See_the_MRF_development图为在旋转坐标系内解绝对速度的控制方程,其中 \vec \omega \times \vec U_i 这项称为科氏力,旋转坐标系内独有的力。他的效果如下面这个视频所示https://haokan.baidu.com/v?vid=4227630901810560602&pd=bjh&fr=bjhauthor&type=video
我的理解是可以将上面的式子理解为绝对速度产生组成的动量的输运方程,其中的通量是相对通量(\vec U_R \vec U_I),同时由于动量是一个矢量,因此在旋转坐标系中还受到科氏力的作用。等式坐标是压力的贡献,和由于运输的物理量U_I的扩散贡献。因此,我在思考是不是诸如湍动能,湍流耗散率这些标量,也可以认为在旋转坐标系内,运输物理量为湍动能,湍流耗散率这些标量,通量为相对速度的通量,但是由于这些量都是标量,因此没有多的项需要添加。另外比如SA模型中的发生项需要计算到voricity的大小,此处的voricity是不是也应该用相对速度?
