Smagorinsky模型系数问题
-
- 李老师,我也没具体看到哪个文章用了这两个默认系数,但搜到一个帖子有个观点,帖子中的超链接无法查看:OpenFOAM大涡模拟湍流模型之Smagorinsky模型代码详解

- 无意中看到一个日本CFD网站,看起来$k_{sgs}$与压力计算值有关。

然后看Smagorinsky的推导,这个推导过程也类似的出现$Ck$和$C_e$参数。疑问依然还是第一种方法是如何计算$k_{sgs}$,如果这个问题知道了,那应该能推断出第一种方法与第二种方法的系数$Ck$和$C_e$的关系。



-
@李东岳 李老师,最近把
Smagorinsky湍流模型两种方式植入方式再梳理了下,下面只讨论不可压缩湍流情况,重新完整总结如下(由于有的公式latex显示异常,就采用截图形式):1. OpenFOAM中LES求解方程形式
根据 【OpenFOAMv2012】Smagorinskyの解説 | mtk_birdman's blog
,对于不可压缩湍流,OpenFOAM中求解的方程如下

其中,
\begin{equation}
\nu_{eff}=\nu+\nu_{sgs} \tag{3}
\end{equation}\begin{equation}
\overline{P}=\overline{p}+\frac{2}{3}\rho k_{sgs} \tag{4}
\end{equation}在OpenFOAM中,不可压缩湍流的 $\rho=1$
【讨论1】
- OpenFOAM中看起来是将 $\overline{P}=\overline{p}+\frac{2}{3}\rho k_{sgs}$作为整体计算,最后的压力计算结果并没有减去 $\frac{2}{3}\rho k_{sgs}$。因此OpenFOAM中LES计算得到的压力并不是真实的压力,其偏差程度取决于 $k_{sgs}$的大小。
- 因此,OpenFOAM中只要不同亚格子模型得到的 $\nu_{sgs}$的值相同,那么其压力结果理论上也应相同,因为 $k_{sgs}$不参与最终的压力计算。
类似的问题在RANS模型也有,OpenFOAM也是把
k忽略掉了,详见下面两个帖子的讨论
OpenFOAM 不可压缩湍流模型的 divDevReff 函数 | Giskard's CFD Learning Tricks
Calculating divDevReff - Page 2 -- CFD Online Discussion Forums
上面两个帖子针对OpenFOAM中RANS模型没有减去k有2个观点:
第1个观点是k对于压力的计算结果影响很小因此可以省去。
第2个观点是将k放到了压力项中一起计算,但OpenFOAM最后没有把压力减去k,究竟k对于压力结果影响大小是未知的。
2. 符号定义与2个假设
解析应变率张量(resolved-scale strain rate tensor):
$$\begin{equation}
\mathbf{\bar{D}}=\frac12\Big(\nabla\mathbf{\bar{U}}+\nabla\mathbf{\bar{U}}^\mathrm{T}\Big) \tag{5}
\end{equation}$$亚格子应力张量(subgrid scale stress tensor):
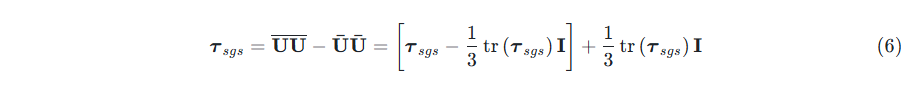
其中 $k_{sgs}$定义为
\begin{equation}
k_{sgs}=\frac12\operatorname{tr}\left(\boldsymbol{\tau}_{sgs}\right) \tag{7}
\end{equation}
根据Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION,有两个假设:
-
Assumption 1: Eddy viscosity approximation,并根据式(7),可得到
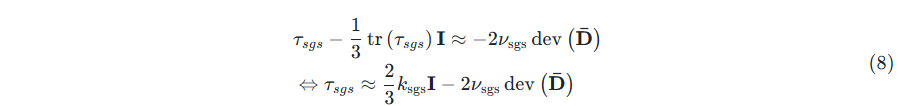
-
Assumption 2: Local equilibrium(assumption of the balance between the subgrid scale energy production and dissipation)
\begin{equation}
P=\varepsilon\Leftrightarrow\overline{\mathbf{D}}:\mathbf{\tau_{sgs}}+C_\varepsilon\frac{k_{\mathrm{sgs}}^{1.5}}\Delta=0 \tag{9}
\end{equation}
其中局部平衡假设公式参考资料:
- 《Sullivan, P.P., J.C. McWilliams and C. Moeng, A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorology, 1994. 71: p. 247-276.》

- 【OpenFOAMv2012】Smagorinskyの解説 | mtk_birdman's blog

3. 第2种方法(OpenFOAM的植入方式)讨论
若直接根据 Local equilibrium 假设求解式(9),存在2个未知数: $\nu_{sgs}$,$k_{sgs}$,因此还需要构造 $\nu_{sgs}$和 $k_{sgs}$的关系式:
$$\begin{equation}
\nu_{\mathrm{sgs}}=C_k\Delta\sqrt{k_{\mathrm{sgs}}} \tag{10}
\end{equation}$$事实上,式(10)额外增加了未知数$C_k$,但这最后是作为经验参数直接输入,需要根据不同的模拟流场类型改变。
式(10)来源可参考《Sullivan, P.P., J.C. McWilliams and C. Moeng, A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorology, 1994. 71: p. 247-276.》

根据Smagorinsky SGS model in OpenFOAM | CFD WITH A MISSION,接着将式(8)和(10)代入式(9),就可求解 $k_{sgs}$,再将 $k_{sgs}$代入式(10)可求得 $\nu_{sgs}$。
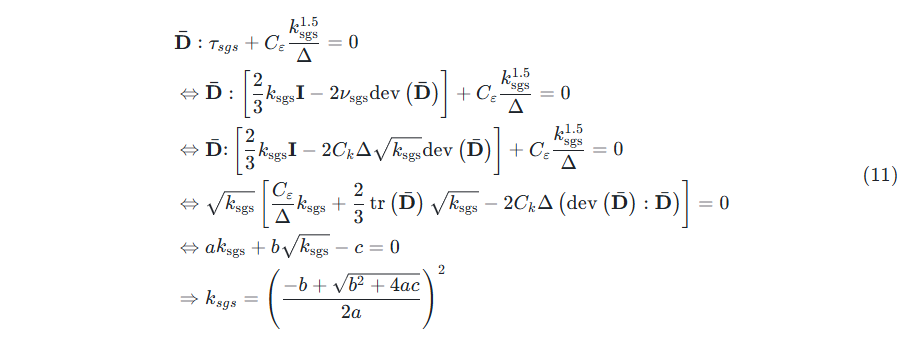
式中,
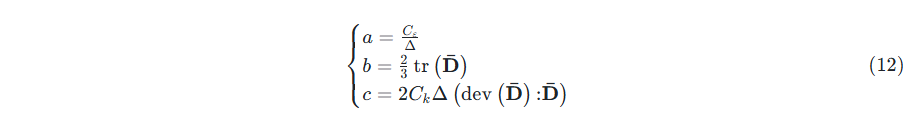
对于不可压缩湍流,式(12)化简为:
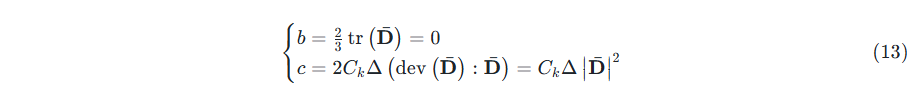
式中,
\begin{equation}
\left|\bar{\mathbf{D}}\right|=\sqrt{2\bar{\mathbf{D}}:\bar{\mathbf{D}}} \tag{14}
\end{equation}把式(13)代入式(11),得到
\begin{equation}
k_{\mathrm{sgs}}=\frac ca=\frac{C_k\Delta^2\left|\overline{\mathbf{D}}\right|^2}{C_\varepsilon} \tag{15}
\end{equation}\begin{equation}
\nu_{\mathrm{sgs}}=C_k\Delta\sqrt{k_{\mathrm{sgs}}}=C_k\sqrt{\frac{C_k}{C_\varepsilon}}\Delta^2\left|\overline{\mathbf{D}}\right| \tag{16}
\end{equation}式(16)对比第1种方法式(18),可得到关系式:
\begin{equation}
C_s=\left ( C_k \sqrt{\frac{C_k}{C_\varepsilon} } \right ) ^{1/2} \tag{17}
\end{equation}OpenFOAM中,默认系数设置为 $C_\varepsilon=1.048,C_k=0.094\Rightarrow C_s=0.1678$, $C_s=0.1678$这个数值是从均匀各向同性湍流推导出来的。
https://www.openfoam.com/documentation/guides/latest/doc/guide-turbulence-les-smagorinsky.html

【讨论2】
- 对于不可压缩湍流,式(13)的化简是基于 $\mathrm{div}(\bar{\mathbf{U} })=0$得到的,但根据 pisoFoam计算的{U},求div(U)结果为何不是严格等于0, $\mathrm{div}(\bar{\mathbf{U}})$实际上并不严格等于0,化简的式(15)与原公式(11)不是严格等价的。
【讨论3】
《Sullivan, P.P., J.C. McWilliams and C. Moeng, A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorology, 1994. 71: p. 247-276.》对第2种方法评价:
An alternative SGS model is to solve the TKE equation explicitly. Advantages of such models are that no equilibrium assumption is required, and the prognostic equation provides a direct means of calculating the SGS kinetic energywhich is needed to construct the actual pressure.-
Sullivan(1994)对第2种方法评价,意思是根据式(4),真实的压力应减去 $k_{sgs}$,即 $\overline{p}=\overline{P}-\frac23\rho k_{\mathrm{sgs}}$。但OpenFOAM求解的是$\overline{P}=\overline{p}+\frac23\rho k_{\mathrm{sgs}}$,所以无论 $k_{sgs}$实际值是多少,只要 $\nu_{sgs}$是相同的,那么得到压力结果也会是相同的。
-
这也正是为何我们只要控制$C_s=\left ( C_k \sqrt{\frac{C_k}{C_e} } \right ) ^{1/2} $为固定值0.065,即使改变 $C_k$值使得 $k_{sgs}$值很大,得到的压力结果也差别不大。但此时我们如果求解析$k_{resolved}$占比,就会对结论产生很大的影响。
-
当$C_s=\left ( C_k \sqrt{\frac{C_k}{C_e} } \right ) ^{1/2} $设置为固定值,根据式(16),$\nu_{sgs}$也为固定值。根据$k_{\mathrm{sgs}}=\left(\frac{\nu_{sgs}}{C_k\Delta}\right)^2$,此时只要 $C_k$取值很小,$k_{sgs}$的值就会很大,但计算的解析$k_{resolved}$基本不变,因此解析湍流能占比就会很小。但如果$C_k$取值很大,$k_{sgs}$的值就会很小,解析湍流能占比就会较大。所以检查LES的解析湍动能占比,Smagorinsky模型经验系数选择有很大影响。
-
为什么第2种方法结果是满足局部平衡假设,还会出现上述问题?原因是 $\nu_{\mathrm{sgs}}=C_k\Delta\sqrt{k_{\mathrm{sgs}}}$这个关系式是一个假设关系,对于不同湍流,$C_k$应有一个合理取值范围,而不能任意取,需要通过实验进行校准。
4. 第1种方法讨论
第1种方法的植入如式(18)所示。
$$\begin{equation}
\nu_{\mathrm{sgs}}=\left(C_s\Delta\right)^2\sqrt{2\bar{\mathbf{D}}:\bar{\mathbf{D}}}=\left(C_s\Delta\right)^2\left|\bar{\mathbf{D}}\right| \tag{18}
\end{equation}$$第1种方法只能设置$C_s$一个参数得到合理的$\nu_{sgs}$,但无法直接得到$k_{sgs}$。但OpenFOAM最后求解得到的压力是$\overline{P}=\overline{p}+\frac23\rho k_{\mathrm{sgs}}$,所以没有求解$k_{sgs}$也对结果无影响。
【讨论4】
$k_{sgs}$的定义如式(7)所示,因此要求解$k_{sgs}$得从求解 $\tau_{sgs}$ 入手。根据式(8),目前未知数有2个未知数:$k_{sgs}$,$\tau_{sgs}$。与第2种方法不同的地方,我们现在是已知$\nu_{sgs}$,求解$k_{sgs}$。再根据 Local equilibrium,式(11)的前2行:
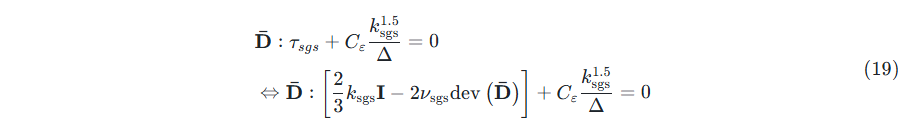
结果发现式(19)中仍然还有2个未知数:$k_{sgs}$, $C_\varepsilon$
因此,第1种方法要求解$k_{sgs}$,还需要输入系数$C_\varepsilon$。
或者输入系数$C_k$,根据 $\nu_{\mathrm{sgs}}=C_k\Delta\sqrt{k_{\mathrm{sgs}}}$反算$k_{sgs}$。注意这里的$C_k$与$C_s$并不直接等价。
【讨论5】
第1种方法:已知$\nu_{sgs}$
- 输入系数$C_\varepsilon$,根据式(19)就能求解$k_{sgs}$。这个时候计算结果自然满足Local equilibrium假设。
- 或者输入系数$C_k$,根据 $\nu_{\mathrm{sgs}}=C_k\Delta\sqrt{k_{\mathrm{sgs}}}$反算$k_{sgs}$。再将$\nu_{sgs}$,$k_{sgs}$代入式(19)就能求解满足Local equilibrium假设的系数$C_\varepsilon$
- 因此Sullivan(1994)对第1种方法的评价是:which results from an assumed local equilibrium balance between shear production and dissipation in the SGS turbulent kinetic energy (TKE) equation.
第2种方法:已知 $C_k,C_\varepsilon$
- 根据式(11)求解$k_{sgs}$ ,结果自然满足Local equilibrium假设。
综上,Smagorinsky湍流模型的2种植入方式都可以满足Local equilibrium假设。
5. 总结
- 第1种方法只设置1个参数$C_s$只能得到$\nu_{sgs}$,要求解$k_{sgs}$还需要额外指定系数$C_k$或者$C_\varepsilon$。
- 第2种方法通过设置2个参数$C_k,C_\varepsilon$,可以得到$\nu_{sgs}$,$k_{sgs}$,但同样的等价$C_s=\left ( C_k \sqrt{\frac{C_k}{C_\varepsilon} } \right ) ^{1/2} $前提下,$C_k$系数的不同取值对$k_{sgs}$影响很大。
- OpenFOAM求解的是$\overline{P}=\overline{p}+\frac23\rho k_{\mathrm{sgs}}$,所以只要 $\nu_{sgs}$是相同的,那么得到压力结果也会是相同的。因此第2种方法通过设置 $C_k,C_\varepsilon$得到等价的$C_s=\left ( C_k \sqrt{\frac{C_k}{C_\varepsilon} } \right ) ^{1/2} $,第1个方法设置同样的$C_s$值,此时两种方法的结果是近似等价的。
- 两个方法设置等价的$C_s$值,结果仍有点小差异,主要是因为速度压力耦合求解过程中,$\mathrm{div}(\bar{\mathbf{U}})$实际并不严格等于0,导致两个方法计算的$\nu_{sgs}$有略微差别,但整体结果是很接近的。
- Smagorinsky湍流模型要得到合理的结果,需要确定$C_s,C_k,C_\varepsilon$三者中的任意2个即可。但因为OpenFOAM求解的是$\overline{P}=\overline{p}+\frac23\rho k_{\mathrm{sgs}}$,可以不需要求解$k_{sgs}$的值,因此获得合理结果只要确定合理的$C_s$即可。
- 目前模拟
channel flow,用的比较多取值是$C_s=0.065$。对应的,OpenFOAM自带算例planeChannel建议系数取值为$C_k=0.0265463553,C_\varepsilon=1.048$
根据《Moin, P. and J. Kim, Numerical investigation of turbulent channel flow. Journal of fluid mechanics, 1982. 118: p. 341-377.》,建议取
Cs=0.065

/OpenFOAM-v2206/tutorials/incompressible/pimpleFoam/LES/planeChannelSmagorinskyCoeffs { Ce 1.048; Ck 0.0265463553; // Updated to give Cs = 0.065 } -
C coolhhh 被引用 于这个主题
-
@coolhhh 太牛逼了!膜拜!另外关于压力没有减去k的问题,Fluent文档(2022R2版本, Ansys Fluent Theory Guide, p118)里有这样的论述:

文献是《G. Erlebacher, M. Y. Hussaini, C. G. Speziale, and T. A. Zang. "Toward the Large-Eddy Simulation
of Compressible Turbulent Flows". J. Fluid Mech. 238. 155–185. 1992.》,是否可以认为k就是忽略了


