势流算法问题
-
东子老师在势流算法中说:进口给定零法向梯度边界条件,但公式(6)里面不是0,,还出现了cells位置的梯度值,不知道是笔误还是啥,一下子看不懂了
势流算法地址 http://dyfluid.com/potentialFoam.html

-
@李东岳 东子老师,您新写的这一版解答了我几乎所有的疑问,感动到泪崩。还有几个小问题想请教您:
①第一张图红框位置应该是出口的Φ值,没有▽吧?
②我按源项=u_inlet和=0对方程(11)进行求解,求解过程为:
入口处,
又
故:
由可求出c2
看上去好像确实可以求出来,但入口处Φ的梯度已经是0了,和方程(7)不一样,两个方程式如何等价的呢?
③第二张图第一个红框应该是▽Φ的通量吧?第二个红框为啥等于0呢?U_f按方程(17)区分了边界和内部,只有内部的速度为0,边界速度不为0,为啥加和就为0了呢?对于第三个红框,由“速度=速度势的梯度”不应该得到▽Φ的通量守恒吗?


-
哪个第一个图?
另外,按照 http://dyfluid.com/potentialFoam.html 上面写的,目前我们要证明的是,链接里面的方程10(进口固定梯度,出口固定值),与方程11(进口零法向梯度,出口固定值,附加源项)的等价。考虑4网格系统,方程10与11离散出来的矩阵都是:
\begin{equation}
\begin{bmatrix}
1 & -1 & & \\
-1 & 2 & -1 & \\
& -1 & 2 & -1 \\
& & -1 & 3 \\
\end{bmatrix}
\begin{bmatrix}
\Phi_1 \\
\Phi_2 \\
\Phi_3 \\
\Phi_4 \\
\end{bmatrix} \equiv
\begin{bmatrix}
u_{inlet} \\
0 \\
0 \\
v \\
\end{bmatrix}
\end{equation} -
@李东岳 东子老师,问题1、系数矩阵第四行我算出来是-1和1,计算过程是这样的:
同样考虑4网格系统
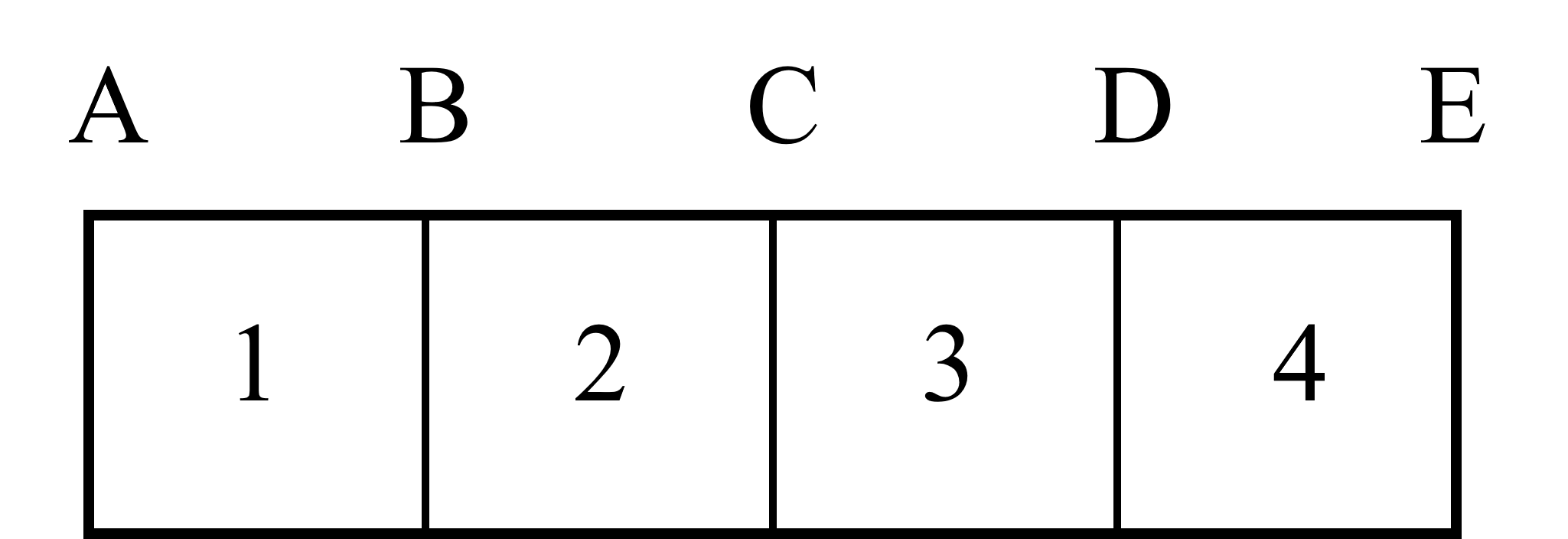
系数矩阵前三行我算的和您一样,对于第4个网格,方程(10)可以离散为
所以第四行系数矩阵应该为-1和1吧,不知道我这样算是不是对的?
问题2、根据公式(3),A处梯度值前面应该有个负号吧?
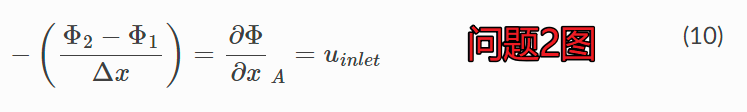
问题3、 红框位置应该是出口的Φ值,没有▽吧?

问题4、第一个红框应该是▽Φ的通量吧?第二个红框为啥等于0呢?U_f按方程(17)区分了边界和内部,只有内部的速度为0,边界速度不为0,为啥加和就为0了呢?对于第三个红框,由“速度=速度势的梯度”不应该得到▽Φ的通量守恒吗?

细节问题有点多哈,麻烦东子老师了 -
哪个第一个图?
另外,按照 http://dyfluid.com/potentialFoam.html 上面写的,目前我们要证明的是,链接里面的方程10(进口固定梯度,出口固定值),与方程11(进口零法向梯度,出口固定值,附加源项)的等价。考虑4网格系统,方程10与11离散出来的矩阵都是:
\begin{equation}
\begin{bmatrix}
1 & -1 & & \\
-1 & 2 & -1 & \\
& -1 & 2 & -1 \\
& & -1 & 3 \\
\end{bmatrix}
\begin{bmatrix}
\Phi_1 \\
\Phi_2 \\
\Phi_3 \\
\Phi_4 \\
\end{bmatrix} \equiv
\begin{bmatrix}
u_{inlet} \\
0 \\
0 \\
v \\
\end{bmatrix}
\end{equation}老师,方程(11)和进口固定梯度,出口固定值得到的矩阵我又手算了一遍。对于4网格系统:
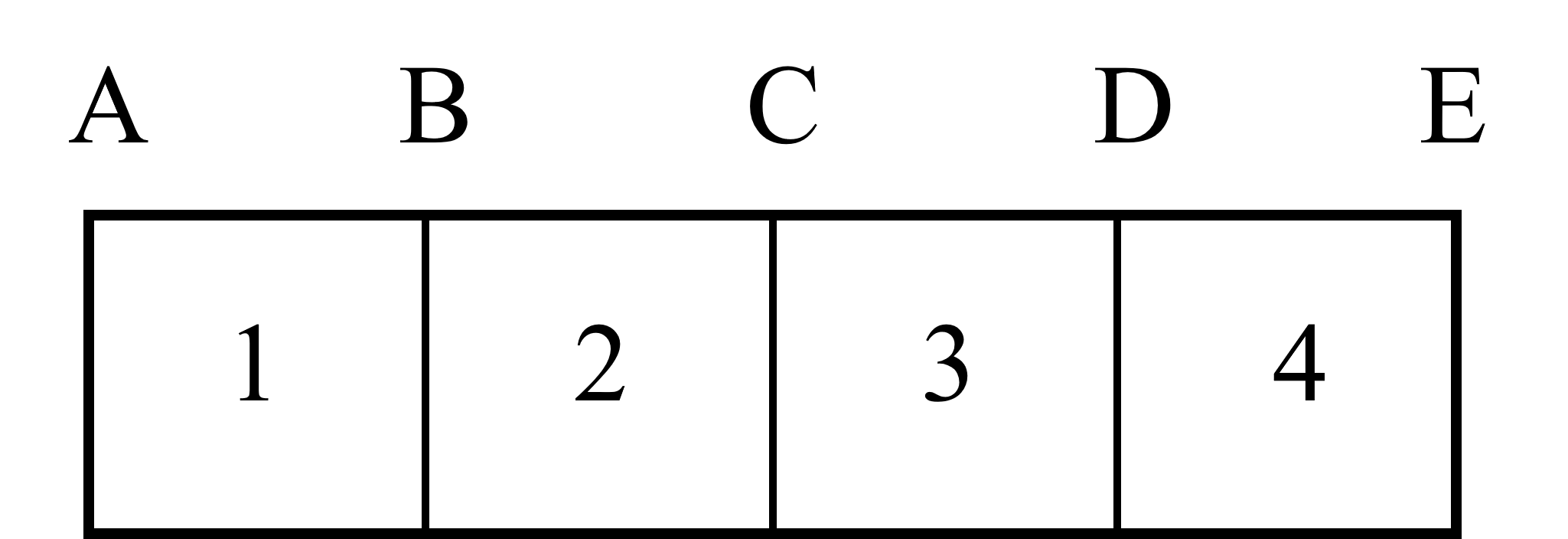
1. 进口固定梯度,出口固定值
边界条件:
cell 1:
cell 2:
同理cell 3:
cell 4:
矩阵为:
2. 方程(11)
边界条件:
cell 1:
cell 2:
同理cell 3:
cell 4:
矩阵为:
和您算的系数矩阵第四行不一致,和等号右边的第一行和第四行也不一致,但计算过程我检查了好几遍,也没发现问题,问题出在哪儿了?





